さて、電磁場テンソルを
とし、電磁場テンソルと前述のマクスウェル方程式(ⅰ) (ⅱ)(ⅲ) (ⅳ)の関係を確かめてみましょう。
電磁ポテンシャルの4元ベクトルを、
とおけば、電磁場テンソルの各成分は、
であり、対角成分は0となりますから、結局、
となります。すると、
となり、ここで、電流密度の4元ベクトルを
とすれば、マクスウェル方程式より、
ですから、結局、(狭義の)マクスウェル方程式は、電磁場テンソルを用いて、
と書けます。
電磁場テンソルとマクスウェル方程式の関係と双対になる関係を見てみます。
まず、双対電磁場テンソルは、
です。ここで、 は4次元のエディントンのイプシロンと呼ばれ、
は4次元のエディントンのイプシロンと呼ばれ、
なる完全反対称反変テンソルであり、共変テンソルの時は
となります。
となり、ビアンキ恒等式より、
ですから、結局、ビアンキ恒等式は、電磁場テンソルを用いて、
と書けます。













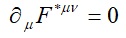
0 件のコメント:
コメントを投稿