ここで、半田広宣氏の『2013:人類が神を見る日 アドバンスト・エディション』(第1部第9章p.228~p.230)に登場する自由電子に関するシュレディンガー方程式の解に関する記述を見ておきましょう。
「さて、このシュレディンガー方程式を解くと、その解となる実際の電子の波動関数のスタイルが導き出される。それが先ほどしめした関数ψ(x, y, z. t)である。果たして、今行った解釈が見当外れではないかどうか、今度はこの解について簡単な分析を試みてみよう。
一見複雑そうに見える数式だが、とりあえず、右式に示したように、この数式をa,b,cの3つの部分に分けて考えてみよう。
aの部分は先述したように確率振幅と呼ばれるもので、この波動自体の振幅を意味する。bの部分は時間を止めたときの空間側側面における波動、cは時間的側面の波動である。b,cそれぞれの波動の原型はオイラーの公式と呼ばれる指数関数にある。オイラーの公式は視覚的イメージとしては下の図4に示したように複素平面上の半径1の双方向の円運動として表される。
さて、まずはbとcの乗数部分を見て欲しい。それぞれの符号が+と-というように互いに逆になっているのがすぐにお分かりになるだろう。これは、b,c両者の回転方向が複素平面上で互いに逆であることを示唆している。第8章の「中心と周縁、ビッグバン理論の欺瞞」のところでも述べたように、時間と空間の持っている逆の方向性がここでは回転方向の相対性として現れているものと考えられる。
では、この場合の逆回転とは具体的に何を意味しているのだろうか。
bのkx・x+ky・y+kz・z(波数と呼ばれる)部分とcのν(振動数)はここでは除外して、大雑把なイメージで捕らえてみよう。
たとえば、今、下図9.9に描いてあるように、複素平面上の定点P(1+0i)から動点Qが左回転を始めたとする。しかし、この運動は絶えず点Pとの比較によって成り立つものであり、相対運動である。逆にこの複素平面自体が原点Oを中心に右回転したとしても見かけ上は全く同じ運動になるだろう。ならば、この時の動点Q
の左回転と、複素平面自体の右回転が、それぞれ空間的側面の波動と時間的側面の波動に相当すると考えられはしないだろうか。
さらに、この関数
は微分しようが積分しようが、その基本的なかたちを変えることがない。そして、その演算は複素平面上での90度ずつの回転として表される。物理学ではこのような回転変換群を1次元ユニタリー群と呼び、U(1)として表す。」
(半田広宣『2013:人類が神を見る日 アドバンスト・エディション』p.228~p.230)
(半田広宣『2013:人類が神を見る日 アドバンスト・エディション』p.229より図.9.9)
ここにある自由電子のシュレーディンガー方程式の解
もこのままの形では見えにくいかもしれません。
もちろん、
ですし、bの指数部分は、
として、
と書けます。また、cの指数部分-i2πνtは、角振動数をωとすれば、ω=2πν と書けますから、
と書けます。すなわち、自由電子のシュレーディンガー方程式の解は、
という見えやすい形となります。つまり、bの指数部分は角波数ベクトルと空間の位置ベクトルの内積となり、cの指数部分は角振動数と時間の積となります。bとcの指数部分はまとめて、
と書けます。これは数学的には、四元角波数ベクトルと四元位置ベクトルのローレンツ内積になります。
今述べたことをここで改めて簡潔にまとめておきましょう。
ここに登場する自由電子に関するシュレディンガー方程式の解というものを、少し見やすくしたものが、以下の自由な平面波の波動関数です。この指数部分、つまり、位相の、第1項の運動量と位置の内積が「空間側の側面」の波動の部分であり、第2項のエネルギーと時間の積が「時間側の側面」の波動の部分ということになります。
ここで、「空間側の側面」内の運動量と位置のマクロ・ミクロ反転の関係と、「時間側の側面」内のエネルギーと時間のマクロ・ミクロ反転の関係を見ておきましょう。









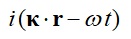



0 件のコメント:
コメントを投稿