さて、自由な平面波は
と表せると言いましたが、オイラーの公式:
からわかるように、この左辺は複素数平面上の単位円を構成するベクトル的な存在でもあり、波で言えば「位相」と呼ばれるθは、単位円周上の点の位置に当たります。そこで、
として、両辺を位相θで微分すれば、
すなわち、
となりますから、位相θで微分することと虚数単位iを掛けることは同等の作用をすることがわかります。ちなみに、2階微分すれば、今度は
すなわち、
となるから、
の一つになっていることがわかります。
ところで、等式(60-7) はどこかで見た形です。実は、これは振動数1で単振動するバネの運動方程式と同じ形になっています。
図60-1 単振動・円運動・正弦関数(佐藤文隆・松下泰雄『波のしくみ』より)
図60-2 単振動するバネ(佐藤文隆・松下泰雄『波のしくみ』より)
実際、質量mのおもりをつけた1次元のバネの単振動の運動方程式は、
の両方の力が釣り合うことから、
と表わせます。ここで、
とおくと、
から、単振動するバネの運動方程式は、
と表わせます。右辺を左辺に移項して演算子をまとめれば、
となりますから、この左辺の演算子部分を因数分解すれば、
となります。したがって、1階の微分方程式
になりますから、これを解けば
という基本解が求まります。これは、前述の等式(60-3)と同型です。見かけ上は、振動に見えるものの背後には、単位円の円運動が隠れているわけです。これは実に興味深いことです。これを図示すると、以下のような感じになります。
図60_3_単振動は回転の射影
このように、理想的なバネにつながれた物体の振動運動、これを「バネの単振動」と呼びますが、ポテンシャル・エネルギーの大きさが中心からの距離の2乗に比例するような振動運動を行う振動子を「調和振動子」と呼びます。v
さて、この単振動するバネの運動方程式を、少し別な観点から変形してみましょう。
(60-8)は、ニュートンの運動方程式の形式での表記でしたが、これをハミルトンの正準運動方程式の形に変形してみましょう。そこで、(60-11)を用いれば、ハミルトンの正準運動方程式は、
と書けます。ここで、係数をまとめて見やすくするために、新しい位置と運動量を
とおけば、
と書けますから、これを行列と列ベクトルを用いて表記すれば、
と書き直せます。ここで、改めて、行列と列ベクトルをゴシック体で、
と表記を変えれば、
と書けますから、この行列方程式を解けば、基本解は、
となりますが、
ですから、行列と列ベクトルを元に戻せば、
と書けます。これは、位置(空間)を横軸、運動量を縦軸にとった平面上の点(X0, P0)を、位相ωtだけ、回転させた点の座標を示しています。
つまり、
「バネの単振動とは、位置-運動量平面上における回転を意味していた」
というわけです。
この位置-運動量相平面が、実2次元平面ではなく、複素数平面だと考えれば、オイラーの公式と関係づけられ、なおかつ、ヌーソロジーにおけるNOOSとNOSの運動としてイメージできないでしょうか。
図60_4. 単位円と永劫回帰を見つめる眼

























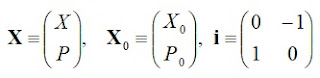

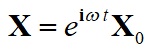



0 件のコメント:
コメントを投稿